統計基礎知識:標本調査の誤差と誤差情報の見方
標本調査の誤差と誤差情報の見方
統計調査の誤差には、ここで説明する標本誤差のほか、非標本誤差というものが存在します。
これは、標本調査のみならず、標本誤差の無い全数調査においても存在するものです。しかしながら、非標本誤差は、以下で述べる無作為抽出を行った場合の標本誤差のように、確率的な評価を行うことが困難であり、誤差を数値的に管理する対象とは一般的にはしないことから、多くの場合には評価されていません。
統計調査のなかで、調べたい対象全体を調べるのではなく、標本すなわち調査対象である世帯や個人、施設などを一部抽出・選定して実施される調査を標本調査といいます。この標本調査では、調査した客体が、全体とは必ずしも一致しないことに起因する標本誤差というものが存在します。すなわち、標本調査の結果として統計表などに示されている結果数値は、この標本誤差を含んだものとして見る必要があります。一般的に標本調査の場合、結果報告書などで、この誤差の程度の情報が表やグラフを用いて提供されています。
ここでは、厚生労働省が実施している国民生活基礎調査を例にとって、標本調査の誤差の意味と報告書等で提供される誤差情報の見方を、以下にできるだけわかりやすく解説します。統計調査の結果を参照される場合の参考にしてください。
標本誤差とはなにか
標本誤差とは、一言で言うと、標本調査の結果として得られた推計値の正確さを表す数値ということになります。この場合の標本調査は調査の客体を無作為に選んだものでなければなりません。
標本調査での調査の客体の選び方には、有意抽出と無作為抽出があります。前者は、恣意的に選んだものであり、後者はランダムに選定したものです。前者の場合は結果の統計的な精度の評価ができないのに対し、後者では確率論を応用して推計値の精度の評価が可能であり、これによる精度管理が必要な場合は、無作為抽出による標本調査を実施することとなります。
標準誤差は、無作為標本調査による推計結果値が真の値からどのくらい離れているかの幅を示す数値です。
無作為抽出により実施した標本調査では、推計値の前後にそれぞれ標準誤差の2倍の値をとると、真の値は約 95パーセントの確率でこの幅の中にあるといえるという性質があるのです。
標準誤差の値が小さいということは、絶対値として小さい幅の中に真の値がはぃっているということであり、逆に標準誤差の値が大きいということは、絶対値として大きな幅の中に真の値があると推測されるということになります。
標本誤差の大きさはなにで決まるのか
では、誤差の大きさはどのような要因できまるのでしょうか。これは、抽出の方法(無作為抽出の方法という意味)や調査対象とした集団の性質など、様々な要因により影響をうけますが、最も関連性を持つのが「標本数の大きさ」、すなわち、調査の客体としたサンプル数です。
例えば、同一の調査、同一の項目においては、サンプル数が多い程標準誤差は小さくなり、逆に、サンプル数が少ない程標準誤差は大きくなります。
調査の標本設計と誤差
さて、一般的には、標本誤差を小さくなるようにしたほうが、推計値の精度が上がることから、標本誤差の観点からは、サンプル数を増やして調査を行うほうが望ましいことになります。しかし一方では、サンプル数が増加すると調査の手間や経費などが増加するため、むやみにサンプル数を増やすわけにはいきません。
従って、サンプル数の決定は、誤差の大きさとコストなどとの兼ね合いということになります。
このころあい、すなわち、その標本調査の推計値の標本誤差をどの程度におさめて、サンプル数をいくつにするかというのが、標本調査の企画における重要な部分になりますが、これを「標本設計」とよんでいます。
国が実施している調査では、見たい項目についての誤差の程度、標準誤差率を5パーセント程度におさめるようにする設計が行われているのが多いといえます。
標準誤差の見方
標本調査による統計調査の報告書には、一般的に標本誤差の情報が提供されていますが、それは主要項目の推計値についての標準誤差と標準誤差率の表によるのが通例です。
まず、前者の見方について、平成15年国民生活基礎調査の報告書を例にとって説明します。
同報告書には、次のような表があります。その一部を次に示します。
なお、全体はこちら(PDF)をご覧ください。
表1 各項目別にみた全国推計値、標準誤差及び標準誤差率
| 項目 | 推計値 (千世帯) | 標準誤差 (千世帯) | 標準誤差率 (%) |
|---|---|---|---|
| 全世帯 | 45800 | 351.6 | 0.77 |
| 雇用者世帯 | 26824 | 281.1 | 1.05 |
| ...... | ..... | ..... | ..... |
| 母子世帯 | 569 | 33.1 | 5.81 |
上の表の全世帯の推計数4580万世帯が、この調査による全国の世帯数の推計値です。
この推計値の誤差として、その右に、標準誤差351.6千世帯というのがありますが、これが調査結果である全国の世帯数の推計値の誤差の大きさをあらわしています。
すなわち、この表によれば、全国の世帯数の真の値は、約95パーセントの確率で、次の幅のなかにあるということがわかります。
45800-2x351.6 =45096.8千世帯
45800+2x351.6 =46503.2千世帯
標準誤差率とはなにか
では、次に、上の表1で出てきた標準誤差率について説明します。
この率は、標本誤差が推計値に対して相対的にどの程度の大きさであるかを示す指標、率というものです。
計算は、次の式になります。
標準誤差率(%)=標準誤差/推計値x100
上の全世帯の例では、351.6/45800x100=0.767685 となります。
この標準誤差率が必要となる理由ですが、例えば、表1で標準誤差は、全世帯数では351.6千世帯であり、母子世帯では33.1千世帯ですので、母子世帯の標準誤差のほう幅が小さいものとなっています。
しかしながら、母子世帯は全世帯に比べて推計値自体が小さいため、標準誤差どうしを比較するのではなくて、推計値との相対関係で、誤差がどの程度の大きさとなっているかを見ることが必要です。これを表したのが標準誤差率です。
表1によれば、全世帯の標準誤差率は0.77%であり、一方の母子世帯は、5.81%となっています。これから、母子世帯の推計値のほうが5.81%と推計値との対比で見た場合、全世帯の推計値よりも大きい誤差をもっているということになります。
標準誤差率の見方
標準誤差率は前記のように計算され、率によってみることとなります。
この指標についても、標準誤差と同様に、推計値を基準(100%)として、その前後にそれぞれ標準誤差率の2倍の幅をとると、この幅のなかに、真の値が約95パーセントの確率で存在するということが言えます。
全国推計数と標準誤差率
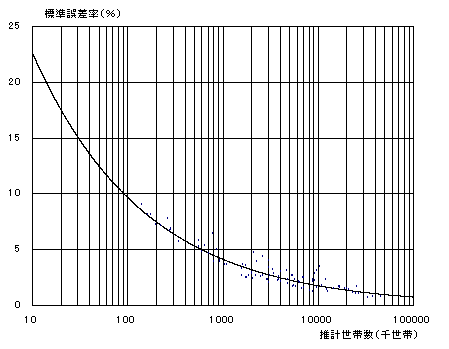
次の図1は、各項目ごとの全国推計世帯数とその標準誤差をグラフのなかにプロットしたものです。
さらに、推計世帯数の大きさ別の標準誤差率を平均的に評価するために傾向線を引いてあります。
したがって、表1の結果を視覚的にとらえることができるほか、表1に掲載されてない項目の誤差についても大体の目安とすることができます。
図1
標本調査の誤差情報提供
このページでは、厚生統計調査で、標本調査として実施されているものについて、誤差情報の追加情報を提供しています。
各標本統計調査の誤差情報は、当該調査報告書で提供されていますので、そちらをご覧ください。
厚生統計テキストブックについて
当協会では、初心者向けの厚生統計入門書として「厚生統計テキストブック第7版」を販売しております。
2020年2月20日より平成26年に発売した厚生統計テキストブック第6版から、最新の統計制度改正、組織編成等を大幅更新した待望の第7版が発売!
厚生統計についてわかりやすくコンパクトに説明しておりますので、厚生統計の参考書としておすすめです。
詳しくはこちら






